Pembahasan Matematika No. 6 - 10 TKD Saintek SBMPTN 2016 Kode Naskah 225

Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2016 kode naskah 225 nomor 6 sampai dengan nomor 10 tentang:

• suku banyak, 
• fungsi eksponen, 
• limit fungsi, 
• barisan dan deret, serta 
• titik stasioner dan nilai ekstrem.

Soal No. 6 tentang Suku Banyak

Diketahui sisa pembagian suku banyak f(x) − g(x) oleh x² + x − 2 adalah x, sisa pembagian f(x) + g(x) oleh x² − 3x + 2 adalah x + 1, maka sisa pembagian (f(x))² + (g(x))² oleh x − 1 adalah ….

A.   5/2
B.   5/4
C.   1/4
D.   1
E.   4

Pembahasan

Mari kita pahami kembali teorema sisa berikut ini!

Jika f(x) dibagi oleh x − a
maka sisanya adalah f(a)

Berdasarkan teorema sisa tersebut, sisa pembagian (f(x))² + (g(x))² oleh x − 1 adalah:

(f(1))² + (g(1))²

Itulah yang ditanyakan. Berarti kita tinggal mencari nilai dari f(1) dan g(1).

Mari kita perhatikan pernyataan pada soal di atas!

Sisa pembagian suku banyak f(x)− g(x) oleh x² + x − 2 adalah x.

Pembagi suku banyak tersebut berbentuk kuadrat yang dapat difaktorkan menjadi:

x² + x − 2 = (x + 2)(x − 1)

Artinya, jika f(x)− g(x) dibagi x² + x − 2 bersisa x, maka dibagi (x + 2) atau (x − 1) pun juga akan bersisa x.

Karena kita butuh nilai f(1) dan g(1) maka kita gunakan pembagi (x − 1). Sehingga sisa pembagian ini adalah:

f(1)− g(1) = 1    … (1)

Sekarang kita perhatikan pernyataan berikutnya.

Sisa pembagian f(x) + g(x) oleh x² − 3x + 2 adalah x + 1.

Faktor pembaginya adalah:

x² − 3x + 2 = (x − 1)(x − 2)

Kita gunakan faktor pembagi (x − 1) sehingga sisa pembagian ini adalah:

f(1) + g(1) = 1 + 1
f(1) + g(1) = 2    … (2)

Nah, sekarang kita eliminasi persamaan (1) dan (2).

f(1)− g(1) = 1
f(1) + g(1) = 2
⎯⎯⎯⎯⎯⎯⎯⎯⎯  +
         2f(1) = 3
           f(1) = 3/2

Substitusi f(1) = 3/2 ke persamaan (2).

f(1) + g(1) = 2
 3/2 + g(1) = 2
           g(1) = 1/2

Dengan demikian,

(f(1))² + (g(1))² = (3/2)² + (1/2)²
                          = 9/4 + 1/4
                          = 10/4
                          = 5/2

Jadi, sisa pembagian (f(x))² + (g(x))² oleh x − 1 adalah 5/2 (A).

Soal No. 7 tentang Fungsi Eksponen

Grafik y = 3^x+1 − (1/9)^x berada di bawah grafik y = 3^x + 1 jika ….

A.   0 < x < 1
B.   x > 1
C.   x < 0
D.   x > 3
E.   1 < x < 3

Pembahasan

Misalkan:

y₁ = 3^x+1 − (1/9)^x
    = 3 . 3^x − 3^−2x
y₂ = 3^x + 1

Karena y₁ berada di bawah y₂ maka nilai y₁ kurang dari y₂.

                y₁ < y₂
3 . 3^x − 3^−2x < 3^x + 1

Agar lebih enak dipandang, kita misalkan p = 3^x. diperoleh:

3p − p⁻² < p + 1
2p − p⁻² − 1 < 0

Selanjutnya, masing-masing suku kita kalikan dengan p², tujuannya supaya tidak mengandung pangkat negatif.

2p³ − 1 − p² < 0
2p³ − p² − 1 < 0

Bentuk terakhir ini adalah suku banyak berderajat tiga. Penyelesaiannya bisa dengan cara Horner seperti soal no. 3 di atas.

Bisa juga dengan memperhatikan koefisiennya. Karena jumlah semua koefisiennya sama dengan nol maka dapat dipastikan salah satu faktornya adalah (p − 1). Sehingga bentuk di atas bisa diubah menjadi:

(p − 1)(2p² + p + 1) < 0

Faktor kedua, yaitu 2p² + p + 1, ternyata tidak dapat difaktorkan lagi. Berarti definit positif sehingga dapat diabaikan.

p − 1 < 0
       p < 1

Sekarang kita kembalikan nilai p = 3^x.
3^x < 1
3^x < 3⁰
  x < 0

Jadi, y₁ berada di bawah y₁ jika x < 0 (C).

Soal No. 8 tentang Limit Fungsi

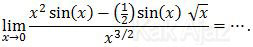
A.   −∞
B.   −7/2
C.   −5/2
D.   −3/2
E.   −1/2

Pembahasan

Limit fungsi trigonometri mendekati nol berlaku hubungan:

x = sin ⁡x = tan⁡ x

Dengan memanfaatkan hubungan tersebut, mari kita ganti sin⁡ x pada soal di atas dengan x.

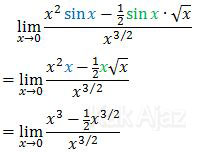
Masing-masing suku dibagi x^3/2, diperoleh:

Nah, sekarang tinggal memasukkan x = 0.

= 0 − 1/2
= −1/2

Jadi, nilai dari limit fungsi tersebut adalah −1/2 (E).

Soal No. 9 tentang Barisan dan Deret

Misalkan (a_n) adalah barisan geometri yang memenuhi sistem a₂ + a₅ − a₄ = 10, a₃ + a₆ − a₅ = 20. Nilai dari a₂ adalah ….A.   −2
B.   −1
C.   0
D.   1
E.   2

Pembahasan

a_n yang dimaksud pada soal adalah suku ke-n barisan geometri yang dirumuskan:

a_n = arⁿ⁻¹

Berpedoman pada rumus tersebut maka:

a₂ + a₅ − a₄ = 10
ar + ar⁴ − ar³ = 10 … (1)

a₃ + a₆ − a₅ = 20
ar² + ar⁵ − ar⁴ = 20 … (2)

Mari kita bandingkan persamaan (1) dan (2)!

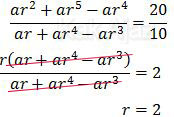
Substitusi r = 2 ke persamaan (1).

ar + ar⁴ − ar³ = 10
2a + 16a − 8a = 10
                 10a = 10
                     a = 1

Dengan demikian,

a₂ = ar
     = 1×2
     = 2

Jadi, nilai dari a₂ adalah 2 (E).

Soal No. 10 tentang Titik Stasioner dan Nilai Ekstrem

Jika f(x) = x³ − 3x² + a memotong sumbu y di titik (0, 10) maka nilai minimum f(x) untuk x ∈ [0, 1] adalah ….A.   10
B.   8
C.   6
D.   4
E.   3

Pembahasan

f(x) memotong sumbu y di titik (0, 10) artinya f(0) = 10.

f(x) = x³ − 3x² + a
f(0) = 0³ − 3.0² + a
  10 = a

Sehingga fungsi lengkap dari f(x) adalah:

f(x) = x³ − 3x² + 10

Fungsi f(x) akan mencapai nilai minimum apabila turunan fungsi tersebut sama dengan nol.

       f'(x) = 0
3x² − 6x = 0
  x² − 2x = 0
 x(x − 2) = 0
x = 0 atau x = 2

Karena x ∈ [0, 1] maka x = 2 tidak memenuhi.

Selanjutnya kita cari nilai dari f(0) dan f(1) untuk menentukan nilai minimumnya.

f(x) = x³ − 3x² + 10

f(0) = 0 − 0 + 10
       = 10 (maksimum)

f(1) = 1 − 3 + 10
       = 8 (minimum)

Jadi, nilai minimum f(x) untuk x ∈ [0, 1] adalah 8 (B).

Bagikan Artikel ini