Pembahasan Matematika No. 1 - 5 TKD Saintek SBMPTN 2016 Kode Naskah 225
Jumat, 25 Mei 2018
Tambah Komentar
Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD
Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun
2016 Kode Naskah 225 nomor 1 sampai dengan nomor 5 tentang:
- geometri,
- segitiga trigonometri,
- persamaan trigonometri,
- transformasi geometri, dan
- dimensi tiga.
Soal No. 1 tentang Geometri
Diketahui persegi dengan panjang sisi 12 dan setengah lingkaran dengan diameter pada alas seperti pada gambar.

Garis CE menyinggung lingkaran di titik F. Panjang CE = ….A. 9√2
B. 13
C. 15
D. 9√3
E. 16

Garis CE menyinggung lingkaran di titik F. Panjang CE = ….A. 9√2
B. 13
C. 15
D. 9√3
E. 16
Pembahasan
Konsep dasar untuk memahami soal ini adalah:
Garis singgung lingkaran selalu tegak lurus dengan jari-jari lingkaran.Perhatikan gambar di bawah ini!

Pandang layang-layang OBCF!
CB dan CF adalah garis singgung lingkaran. Karena keduanya berangkat dari titik yang sama maka panjang keduanya juga sama.
CF = CB = 12
Pandang layang-layang OAEF!
EA dan EF adalah garis singgung lingkaran. Anggap saja panjang EF = x, maka:
EA = EF = x
Sehingga panjang CE adalah:
CE = CF + EF
= 12 + x
= 12 + x
Nah, kita tinggal menentukan nilai x.
Sekarang pandang segitiga CDE! Segitiga CDE adalah segitiga siku-siku sehingga berlaku teorema Pythagoras.
CE2 = CD2 + DE2
(12 + x)2 = 122 + (12 − x)2
144 + 24x + x2 = 144 + 144 − 24x + x2
48x = 144
x = 3
(12 + x)2 = 122 + (12 − x)2
48x = 144
x = 3
Dengan demikian,
CE = 12 + x
= 12 + 3
= 15
= 12 + 3
= 15
Jadi, panjang CE adalah 15 (C).
Soal No. 2 tentang Segitiga Trigonometri
Segitiga ABC siku-siku di B. Titik D terletak pada sisi BC
sedemikian hingga CD = 2BD. Jika ∠DAB = 30° maka besar sudut CAD adalah
….A. 15°
B. 20°
C. 30°
D. 45°
E. 50°
B. 20°
C. 30°
D. 45°
E. 50°
Pembahasan
Pertama yang harus dipahami adalah maksud dari CD = 2BD.

Variabel a di atas hanya permisalan. Anda bisa menggunakan variabel x, y, atau yang lain.
Perhatikan ilustrasi untuk soal di atas!

Padang segitiga ABD!

Dengan mengalikan pembilang dan penyebutnya dengan √3, diperoleh:
AB = a√3
Sekarang padang segitiga ABC!

Dengan demikian ∠CAD adalah:
∠CAD = ∠BAC − ∠DAB
= 60° − 30°
= 30°
= 60° − 30°
= 30°
Jadi, sudut CAD adalah 30° (C).
Soal No. 3 tentang Persamaan Trigonometri
Diketahui 2 sin2 t − 2 sin t = 1 − csc t dengan 0 < t <2π, t ≠ π. Banyaknya anggota himpunan penyelesaian dari persamaan di atas adalah ….A. 2
B. 3
C. 4
D. 5
E. 6
B. 3
C. 4
D. 5
E. 6
Pembahasan
Mungkin yang agak asing adalah fungsi csc t. Apa itu csc t?
csc t = cosec t
= 1/(sin t)
= 1/(sin t)
Sehingga persamaan trigonometri di atas dapat diubah menunjukkan:
2 sin2 t − 2 sin t = 1 − csc t
2 sin2 t − 2 sin t = 1 − 1/(sin t)
2 sin2 t − 2 sin t = 1 − 1/(sin t)
Kalikan masing-masing suku dengan sin t.
2 sin3 t − 2 sin2 t = sin t − 1
2 sin3 t − 2 sin2 t − sin t + 1 = 0
2 sin3 t − 2 sin2 t − sin t + 1 = 0
Ternyata membentuk suku banyak berderajat tiga. Sebaiknya kita selesaikan dengan cara Horner.

Berdasarkan metode di atas diperoleh:
sin t = 1
t = 90°
t = 90°
Hasil bagi dari cara Horner tersebut (warna biru) adalah:
2 0 −1 yang berarti:
2 sin2 t − 1 = 0
2 sin2 t = 1
sin2 t = ½
sin t = ±½√2
2 0 −1 yang berarti:
2 sin2 t − 1 = 0
2 sin2 t = 1
sin2 t = ½
sin t = ±½√2
Sampai di sini sebenarnya jawaban sudah bisa ditebak.
Coba perhatikan! Untuk interval 0 < t < 2π, sin t = 1 hanya ada 1 nilai, sin t = ½√2 dan sin t = −½√2 masing-masing mempunyai 2 nilai. Sehingga total nilai t adalah 5.
Baiklah, agar pembahasan lebih panjang, kita selesaikan satu per satu.
sin t = ½√2 (ada di kuadran I dan II)
t1 = 45°
t2 = (180 − 45)°
= 135°
t1 = 45°
t2 = (180 − 45)°
= 135°
sin t = −½√2 (ada di kuadran III dan IV)
t1 = (180 + 45)°
= 225°
t2 = (360 − 45)°
= 315°
t1 = (180 + 45)°
= 225°
t2 = (360 − 45)°
= 315°
Dengan demikian himpunan penyelesaian persamaan trigonometri tersebut adalah:
{45°, 90°, 135°, 225°, 315°}
Jadi, banyaknya anggota himpunan penyelesaian dari persamaan di atas adalah 5 (D).
Soal No. 4 tentang Transformasi Geometri
Jika pencerminan titik P(s, t) terhadap garis x = a yang dilanjutkan dengan pencerminan terhadap garis y = b menghasilkan translasi  maka a + b = ….A. s + t + 20
maka a + b = ….A. s + t + 20
B. 2s + t + 10
C. s + t + 10
D. s + 2t + 10
E. s + t + 5
 maka a + b = ….A. s + t + 20
maka a + b = ….A. s + t + 20B. 2s + t + 10
C. s + t + 10
D. s + 2t + 10
E. s + t + 5
Pembahasan
Pencerminan titik P(x, y) terhadap garis x = h dan y = k masing dirumuskan sebagai:

Berpedoman pada rumus di atas, pencerminan titik P(s, t) terhadap garis x = a adalah:

Hasil dari pencerminan tersebut dicerminkan lagi terhadap garis y = b. Diperoleh:
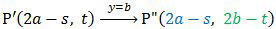
Hasil pencerminan yang terakhir ini sama dengan translasi
 terhadap titik P(s, t).
terhadap titik P(s, t).
Sehingga diperoleh hubungan:
2a − s = s + 10
2a = 2s + 10
a = s + 5
2a = 2s + 10
a = s + 5
2b − t = t + 10
2b = 2t + 10
b = t + 5
2b = 2t + 10
b = t + 5
Dengan demikian,
a + b = (s + 5) + (t + 5)
= s + t + 10
= s + t + 10
Jadi, nilai dari a + b adalah s + t + 10 (C).
Soal No. 5 tentang Dimensi Tiga
Diketahui kubus ABCD.EFGH. titik M berada di rusuk AD sedemikian
sehingga AM : MD = 1 : 2. Titik N berada di rusuk CD sedemikian sehingga
CN : ND = 1 : 2. Titik P berada di rusuk DH sedemikian sehingga DP : PH
= 2 : 1. Jika α adalah sudut antara bidang MNP dan garis PB maka nilai
cos α = ….
A. 5/44 √44
B. 5/33 √33
C. 5/22 √22
D. 1/13 √13
E. 1/11 √11
B. 5/33 √33
C. 5/22 √22
D. 1/13 √13
E. 1/11 √11
Pembahasan
Gambaran kubus yang dimaksud adalah sebagai berikut:

Anggap saja rusuk kubus tersebut adalah 3a (untuk mempermudah penghitungan) sehingga:
AM = CN = PH = a
MD = ND = DP = 2a
MD = ND = DP = 2a
Segitiga MNP adalah segitiga sama sisi dengan panjang rusuk (pandang segitiga MDP):
MP = √(MD2 + DP2)
= √[(2a)2 + (2a)2]
= 2a√2
= √[(2a)2 + (2a)2]
= 2a√2
PQ adalah tinggi segitiga sama sisi MNP. Tinggi segitiga sama sisi dirumuskan:
t = ½√3 × rusuk segitiga
PQ = ½√3 × 2a√2
= a√6
PQ = ½√3 × 2a√2
= a√6
BD adalah diagonal alas kubus yang dirumuskan:
BD = rusuk kubus × √2
= 3a√2
= 3a√2
Sedangkan BQ adalah 2/3 diagonal.
BQ = 2/3 × 3a√2
= 2a√2
= 2a√2
Sekarang tinggal menentukan panjang BP. Pandang segitiga BDP!
BP = √(BD2 + DP2 )
= √[(3a√2)2 + (2a)2]
= √(18a2 + 4a2 )
= a√22
= √[(3a√2)2 + (2a)2]
= √(18a2 + 4a2 )
= a√22
Nah, semua rusuk segitiga BPQ sudah diketahui yang mana sudut α ada di dalamnya.

Kita gunakan aturan kosinus untuk mendapatkan nilai dari cos α.

Variabel a2 bisa dicoret dan √132 = 2√33, sehingga diperoleh:

Jadi, nilai cos α adalah 5/33 √33 (B).


Belum ada Komentar untuk "Pembahasan Matematika No. 1 - 5 TKD Saintek SBMPTN 2016 Kode Naskah 225"
Posting Komentar