Pembahasan Matematika IPA UN 2017 No. 1 - 5

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPA nomor 1 sampai dengan nomor 5 tentang:

• logaritma, 
• perpangkatan, 
• pertidaksamaan eksponen dan logaritma, 
• bentuk akar, serta 
• fungsi kuadrat.

Soal No. 1 tentang Logaritma

Hasil dari

A.   6
B.   12
C.   24
D.   36
E.   48

Pembahasan

Langkah pertama, ubah bentuk penyebutnya dengan menggunakan rumus:

Sehingga bentuk di atas menjadi:

Selanjutnya, ubah semua angka menjadi bilangan berpangkat sehingga diperoleh:

Kemudian gunakan rumus ^amlog⁡ bⁿ = n/m ^alog ⁡b, sehingga menjadi:

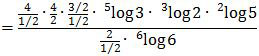
Nah, semua bentuk logaritma di atas hasilnya sama dengan 1. Perhatikan keterangan berikut!

Sekarang tinggal menghitung angka di depannya saja.

Jadi, hasil dari bentuk logaritma di atas adalah 12 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Logaritma.

Soal No. 2 tentang Perpangkatan

Hasil dari

adalah ….A.   2/5
B.   8/25
C.   4/25
D.   8/125
E.   4/125

Pembahasan

Langkah pertama, ubah bilangan pokoknya menjadi bilangan berpangkat.

Selanjutnya, bilangan pokok yang berpangkat negatif kita pindah posisi agar berpangkat positif (atas ke bawah atau sebaliknya).

Nah, sekarang tinggal menjumlahkan pangkatnya.

Jadi, hasil dari bentuk pangkat tersebut adalah 8/25 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Perpangkatan.

Soal No. 3 tentang Pertidaksamaan Eksponen dan Logaritma

Nilai x yang memenuhi pertidaksamaan 3 ∙ 4^x − 7 ∙ 2^x + 2 > 0 adalah ….A.   x < −1 atau x > ²log ⁡3
B.   x < ²log(1/3) atau x > 1
C.   ²log⁡(1/3) < x < 1
D.   x < 1 atau x > ²log(1/3)
E.   1 < x < ²log(1/3)

Pembahasan

Misalkan:

p = 2^x  sehingga  p² = 4^x

Maka pertidaksamaan di atas menjadi:

3p² − 7p + 2 > 0
(3p − 1)(p − 2) > 0

Karena tanda pertidaksamaannya ‘>’ maka hasil penyelesaian bentuk kuadrat tersebut berada di sebelah kiri 1/3 atau di sebelah kanan 2.

p < 1/3  atau  p > 2

Kita kembalikan lagi permisalan di atas.

Jadi, nilai x yang memenuhi pertidaksamaan tersebut adalah opsi (B).

Perdalam materi ini di Pembahasan Matematika UN: Pertidaksamaan Eksponen dan Logaritma.

Soal No. 4 tentang Bentuk Akar

Bentuk sederhana dari

adalah ….A.   5(2√11 − √19)
B.   1/5 (2√11 + √19)
C.   1/5 (2√11 − √19)
D.   −1/5 (2√11 − √19)
E.   −1/5 (2√11 + √19)

Pembahasan

Perhatikan, pembilang berbentuk (a − b)(a + b) yang dapat disederhanakan menjadi a² − b².

(√10 − √5)(√10 + √5) = 10 − 5

Sehingga bentuk akar di atas menjadi:

Sekarang kita kalikan dengan bilangan sekawan dari penyebutnya.

Jadi, bentuk sederhana dari bentuk akar tersebut adalah opsi (C).

Perdalam materi ini di Pembahasan Matematika IPA UN: Bentuk Akar.

Soal No. 5 tentang Fungsi Kuadrat

Jika grafik fungsi y = 2x² + (p − 1)x + 2 menyinggung sumbu x, nilai p yang memenuhi adalah ….

A.   p = 5 atau p = 2
B.   p = −5 atau p = 2
C.   p = 5 atau p = 3
D.   p = −5 atau p = 3
E.   p = 5 atau p = −3

Pembahasan

Syarat menyinggung adalah diskriminan fungsi kuadrat tersebut sama dengan nol.

                      D = 0 
            b² − 4ac = 0
 (p − 1)² − 4∙2∙2 = 0
p² − 2p + 1 − 16 = 0
      p² − 2p − 15 = 0
(p − 5)(p + 3) = 0
      p = 5 atau p = −3

Jadi, nilai p yang memenuhi adalah opsi (E).

Bagikan Artikel ini