Pembahasan Matematika Dasar No. 56 - 60 TKPA SBMPTN 2017 Kode Naskah 226

Pembahasan soal Matematika Dasar Tes Kemampuan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2017 kode naskah 226 nomor 56 sampai dengan nomor 60 tentang:

• sistem pertidaksamaan linear, 
• transformasi geometri, 
• integral fungsi aljabar, 
• limit fungsi, dan 
• kaidah pencacahan.

Soal No. 56 tentang Sistem Pertidaksamaan Linear

Luas daerah penyelesaian sistem pertidaksamaan x + y ≤ 3,3x + 2y ≥ 6, y ≥ 0 adalah … satuan luas.A.   1/2
B.   3/4
C.   1
D.   3/2
E.   2

Pembahasan

Kita tentukan dulu garis-garis pembatas daerah tersebut kemudian kita arsir daerah yang dimaksud.

x + y = 3 (1)		3x + 2y = 6 (2)
x	y	x	y
0	3	0	3
3	0	2	0

Berdasarkan tabel di atas, daerah yang dimaksud adalah:

Ternyata daerah tersebut adalah segitiga dengan:

alas    : a = 1
tinggi : t = 3

dengan demikian, luas daerah tersebut adalah:

L = 1/2 at
   = 1/2 ∙ 1 ∙ 3
   = 3/2

Jadi, luas daerah penyelesaian sistem pertidaksamaan tersebut adalah 3/2 satuan luas.

Soal No. 57 tentang Transformasi Geometri

Titik (1, 0) dengan translasi dan kemudian dicerminkan terhadap garis x = 3 ke titik (6, 2). Peta titik (2, 1) di bawah transformasi yang sama adalah …. A.   (5, 3)
B.   (6, 2)
C.   (6, 3)
D.   (7, 2)
E.   (7, 3)

Pembahasan

Rumus translasi dan pencerminan terhadap garis  x = h masing-masing adalah sebagai berikut: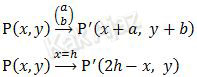

Berdasarkan kedua rumus di atas:

Kemudian titik P’ tersebut dicerminkan terhadap garis x = 3 menjadi P”.

Titik P” ini adalah (6, 2) sehingga diperoleh:

5 − a = 6
    −a = 6 − 5
    −a = 1
      a = −1

Dengan demikian, translasi di atas adalah:

Dengan transformasi yang sama maka bayangan titik Q(2, 1) adalah:

Jadi, peta (2, 1) adalah (5, 3) (A).

Soal No. 58 tentang Integral Fungsi Aljabar

A.   3x − 2x√x + C
B.   2x − 3x√x + C
C.   3x√x − 2x + C
D.   2x√x − 3x + C
E.   3x + 2x√x + C

Pembahasan

Dengan memanfaatkan rumus:

a² − b² = (a + b)(a − b)

salah satu bentuk aljabar di atas dapat disederhanakan.

1− x = 1² − (√x)²
        = (1 + √x)(1 − √x)

Sehingga integral fungsi aljabar di atas dapat diselesaikan menjadi:

Catatan:

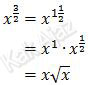
Jadi, hasil integral fungsi aljabar tersebut adalah opsi (A).

Soal No. 59 tentang Limit Fungsi

Jika kurva f(x) = ax² + bx + c memotong sumbu y di titik (0, 1) dan maka (b + c)/a = ….A.   −1
B.   −1/2
C.   0
D.   1
E.   3/2

Pembahasan

Kurva f(x) = ax² + bx + c memotong sumbu y di titik (0, 1). Ini berarti bahwa:

                    f(0) = 1
a ∙ 0² + b ∙ 0 + c = 1
                        c = 1

Sehingga kurva f(x) menjadi:

f(x) = ax² + bx + 1

Jika nilai x = 1 disubstitusi langsung pada maka akan menghasilkan 0/0 sehingga:

                    f(1) = 0
a ∙ 1² + b ∙ 1 + 1 = 0
                  a + b = −1 … (1)

Untuk berlaku:

f' (1) = −4

Kita turunkan dulu fungsi f(x).

f(x) = ax² + bx + 1
f'(x) = 2ax + b
f'(1) = −4
2a + b = −4 … (2)

Selanjutnya kita eliminasi persamaan (1) dan (2).

2a + b = −4
  a + b = −1
⎯⎯⎯⎯⎯⎯⎯⎯  −
        a = −3

Substitusi a = −3 pada persamaan (1) diperoleh:

−3 + b = −1
        b = 2

Dengan demikian,

(b + c)/a = (2 + 1)/(−3)
               = 3/(−3)
               = −1

Jadi, nilai dari (b + c)/a adalah −1 (A).

Soal No. 60 tentang Kaidah Pencacahan

Banyak susunan berfoto berjajar untuk 3 pasang pemain bulu tangkis ganda dengan tidak setiap pemain dan pasangannya berdekatan adalah ….A.   720
B.   705
C.   672
D.   48
E.   15

Pembahasan

Tiga pasang pemain ganda bulu tangkis berarti ada 6 orang. Banyak susunan mereka berfoto berjajar (tanpa syarat) adalah:

6! = 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1
    = 720

Setiap pemain dan pasangannya berdekatan.

• Karena ada 3 pasang pemain maka ketiga pasangan tersebut dapat bertukar posisi sebanyak:

3! = 3 ∙ 2 ∙ 1
    = 6

• Di sisi lain, setiap pasang terdiri dari 2 pemain yang dapat bertukar posisi sebanyak 2 kali (misal posisi AB atau BA). Sehingga banyak cara bertukar posisi yang mungkin dari ketiga pasangan adalah:

2 ∙ 2 ∙ 2 = 8

Dengan demikian, banyak cara setiap pemain dan pasangannya selalu berdekatan adalah:

6 ∙ 8 = 48

Sedangkan banyak susunan 3 pasang dengan tidak setiap pemain dan pasangannya berdekatan adalah:

720 − 48 = 672

Jadi, banyak susunan berfoto tersebut ada 672 cara (C).

Bagikan Artikel ini