Pembahasan Matematika Dasar No. 51 - 55 TKPA SBMPTN 2017 Kode Naskah 226
Jumat, 25 Mei 2018
Tambah Komentar
Pembahasan soal Matematika Dasar Tes Kemampuan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2017 kode naskah 226 nomor 51 sampai dengan nomor 55 tentang:
- barisan dan deret aritmetika,
- aplikasi turunan,
- barisan dan deret geometri,
- fungsi komposisi, dan
- dimensi tiga.
Soal No. 51 tentang Barisan dan Deret Aritmetika
Suku ke-11 suatu barisan aritmetika sama dengan empat kali suku ke-16.
Jika beda barisan tersebut adalah −3 maka empat kali suku ke-14 sama
dengan suku ke- ….A. 1
B. 3
C. 5
D. 7
D. 9
B. 3
C. 5
D. 7
D. 9
Pembahasan
Rumus suku ke-n suatu barisan aritmetika dinyatakan:
Un = a + (n − 1)b
Suku ke-11 sama dengan empat kali suku ke-16.
U11 = 4U16
a + 10b = 4(a + 15b)
a + 10b = 4(a + 15b)
Dengan b = −3 diperoleh:
a − 30 = 4(a − 45)
a − 30 = 4a − 180
150 = 3a
a = 50
a − 30 = 4a − 180
150 = 3a
a = 50
Empat kali suku ke-14 sama dengan suku ke-n.
4U14 = Un
4(a + 13b) = a + (n − 1)b
4(a + 13b) = a + (n − 1)b
Substitusi a = 50 dan b = −2 diperoleh:
4(50 − 39) = 50 + (n − 1)(−3)
4 ∙ 11 = 50 − 3n + 3
44 = −3n + 53
3n = 9
n = 3
4 ∙ 11 = 50 − 3n + 3
44 = −3n + 53
3n = 9
n = 3
Jadi, empat kali suku ke-14 sama dengan suku ke-3 (B).
Soal No. 52 tentang Aplikasi Turunan
Seseorang memelihara ikan di suatu kolam. Rata-rata bobot ikan per ekor pada saat panen dari kolam tersebut adalah (6 − 0,02x) kg, dengan x menyatakan banyak ikan yang dipelihara. Maksimum total bobot semua ikan pada saat panen yang mungkin adalah … kg.
A. 400
B. 420
C. 435
D. 450
E. 465
B. 420
C. 435
D. 450
E. 465
Pembahasan
Rata-rata bobot ikan per ekor pada saat panen:
6 − 0,02x
Total bobot semua ikan pada saat panen:
B(x) = (6 − 0,02x)x
= 6x − 0,02x2
= 6x − 0,02x2
Agar nilai B(x) maksimum maka turunan pertama dari fungsi B(x) harus sama dengan nol.
B(x)' = 0
6 − 0,04x = 0
6 = 0,04x
x = 150
6 − 0,04x = 0
6 = 0,04x
x = 150
Dengan demikian, fungsi B(x) mencapai maksimum pada saat x = 150.
B(x) = 6x − 0,02x2
B(150) = 6 ∙ 150 − 0,02 ∙ 1502
= 900 − 450
= 450
B(150) = 6 ∙ 150 − 0,02 ∙ 1502
= 900 − 450
= 450
Jadi, total bobot maksimum semua ikan pada saat panen yang mungkin adalah 450 kg (D).
Soal No. 53 tentang Barisan dan Deret Geometri
Perbandingan suku ke-6 terhadap suku pertama barisan geometri adalah
1/32. Jika jumlah suku ke-3 dan suku ke-4 adalah 15 maka jumlah 3 suku
pertama barisan tersebut adalah ….
A. 30
B. 40
C. 50
D. 60
E. 70
B. 40
C. 50
D. 60
E. 70
Pembahasan
Suku ke-n barisan geometri dinyatakan sebagai:
Un = arn−1
Perbandingan suku ke-6 terhadap suku pertama barisan geometri adalah 1/32.

Jumlah suku ke-3 dan suku ke-4 adalah 15.
U3 + U4 = 15
ar2 + ar3 = 15
ar2 + ar3 = 15
Substitusi r = 1/2 diperoleh:
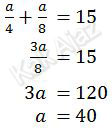
Karena yang ditanyakan jumlah 3 suku pertama, lebih enak dihitung langsung (tanpa rumus Sn).
S3 = a + ar + ar2
= 40 + 20 + 10
= 70
= 40 + 20 + 10
= 70
Jadi, jumlah 3 suku pertama barisan tersebut adalah 70 (B).
Soal No. 54 tentang Fungsi Komposisi
Jika f(x) = 1 − x2 dan g(x) = √(5 − x) maka daerah hasil fungsi komposisi f ∘ g adalah ….
A. {y│−∞ < y < ∞}
B. {y│y ≤ −1 atau y ≥ 1}
C. {y│y ≤ 5}
D. {y│y ≤ 1}
E. {y│−1 ≤ y ≤ 1}
B. {y│y ≤ −1 atau y ≥ 1}
C. {y│y ≤ 5}
D. {y│y ≤ 1}
E. {y│−1 ≤ y ≤ 1}
Pembahasan
Daerah hasil atau range suatu fungsi adalah nilai fungsi tersebut (nilai y) untuk x yang memenuhi.
Untuk menentukan daerah hasil fungsi komposisi f ∘ g, kita harus menentukan dulu nilai x yang memenuhi pada fungsi f dan g sebelum dikomposisikan.
- Fungsi f(x) = 1 − x2 memenuhi untuk semua nilai x.
- Fungsi g(x) = √(5 − x) memenuhi jika nilai yang terdapat dalam akar lebih besar atau sama dengan nol
5 − x ≥ 0Selanjutnya kita tentukan fungsi komposisinya dengan berpatokan pada fungsi f.
−x ≥ −5
x ≤ 5 … (1)
Ini adalah domain atau daerah asal fungsi g yang juga merupakan domain dari fungsi komposisi f ∘ g.
f(x) = 1 − x2
f ∘ g = 1 − [g(x)]2
= 1 − [√(5 − x)]2
= 1 − (5 − x)
= 1 − 5 + x
= x − 4
f ∘ g = 1 − [g(x)]2
= 1 − [√(5 − x)]2
= 1 − (5 − x)
= 1 − 5 + x
= x − 4
Misalkan daerah hasil fungsi komposisi tersebut adalah y, maka:
y = x − 4 … (2)
Nah, sekarang kita gantikan x pada persamaan (2) dengan x pada persamaan (1).
y ≤ 5 − 4
y ≤ 1
y ≤ 1
Jadi, daerah hasil fungsi komposisi f ∘ g adalah {y│y ≤ 1} (D).
Soal No. 55 tentang Dimensi Tiga
Diketahui kubus ABCD.EFGH dengan P dan Q berturut-turut adalah titik tengah HG dan BC.

Jika panjang rusuk kubus tersebut adalah 4 cm maka jarak P ke Q adalah … cm.

Jika panjang rusuk kubus tersebut adalah 4 cm maka jarak P ke Q adalah … cm.
A. 2√3
B. 2√6
C. 6√2
D. 6√3
E. 6√6
B. 2√6
C. 6√2
D. 6√3
E. 6√6
Pembahasan
Perhatikan gambar berikut ini!
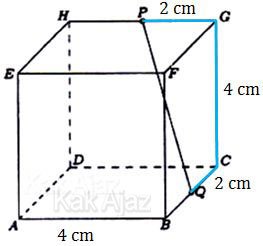
Lintasan terdekat dari titik P menuju Q adalah:
PG – GC – CQ [lintasan biru]
Dengan demikian, panjang PQ adalah:
PQ = √(PG2 + GC2 + CQ2)
= √(22 + 42 + 22)
= √24
= 2√6
= √(22 + 42 + 22)
= √24
= 2√6
Jadi, jarak titik P ke titik Q adalah 2√6 cm (B).


Belum ada Komentar untuk "Pembahasan Matematika Dasar No. 51 - 55 TKPA SBMPTN 2017 Kode Naskah 226"
Posting Komentar