Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2017 Kode Naskah 226

Pembahasan soal Matematika Dasar Tes Kemampuan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2017 kode naskah 226 nomor 46 sampai dengan nomor 50 tentang:

• matriks, 
• pertidaksamaan, 
• geometri, 
• fungsi, dan 
• statistika.

Soal No. 46 tentang Matriks

Misalkan A^T adalah transpos matriks A.

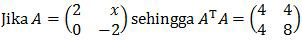
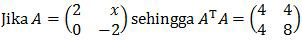
maka nilai x² − x adalah ….

A.   0
B.   2
C.   6
D.   12
E.   20

Pembahasan

Bila tiap komponen baris suatu matriks dipindahkan menjadi komponen kolom maka terbentuklah transpos matriks.

Sehingga,

Dengan demikian, penyelesaian persamaan matriks pada soal di atas adalah:

Ambil saja komponen kanan atas.

2x = 4
  x = 2

Sehingga,

x² − x = 2² − 2
           = 4 − 2
           = 2

Jadi, nilai x² − x adalah 2 (B).

Soal No. 47 tentang Pertidaksamaan

Jika himpunan penyelesaian |2x − a| < 5 adalah {x│−1 < x < 4} maka nilai a adalah ….

A.   −4
B.   −3
C.   −1
D.   3
E.   4

Pembahasan

Pertidaksamaan harga mutlak kurang dari “<” dapat dirumuskan:

|x| < p ⟺ −p < x < p

Berdasarkan rumus di atas maka:

|2x − a| < 5
−5 < 2x − a < 5
−5 + a < 2x < 5 + a
½ (−5 + a) < x < ½ (5 + a)

Sementara itu, diketahui bahwa:

−1 < x < 4

Mari kita bandingkan kedua pertidaksamaan di atas!

½ (−5 + a) < x < ½ (5 + a)
             −1 < x < 4

Dengan membandingkan kedua pertidaksama-an di atas diperoleh:

½ (−5 + a) = −1
       −5 + a = −2
                a = 3

atau

½ (5 + a) = 4
       5 + a = 8
             a = 3

Jadi, nilai a pada pertidaksamaan harga mutlak di atas adalah 3 (D).

Soal No. 48 tentang Geometri

Pada segitiga siku-siku sama kaki ABC, sisi AB dan BC masing-masing terbagi menjadi tiga bagian yang sama, berturut-turut oleh titik K, L, dan M, N.

Jika luas ∆ABC adalah x cm² maka luas ∆KMN adalah … cm².

A.   x/3
B.   2x/9
C.   x/9
D.   x/18
E.   x/36

Pembahasan

Perhatikan gambar berikut ini!

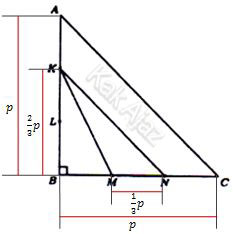
Pandang ∆ABC!

Alas    : a = p
Tinggi : t = p

Diketahui luas ∆ABC adalah x sehingga:

         L = x
    ½ at = x
½ p . p = x
       p² = 2x    ... (1)

Sekarang pandang ∆KMN!

Alas    : a = ⅓ p
Tinggi : t = ⅔ p

Sehingga luas ∆KMN adalah:

L = ½ at
   = ½ ∙ ⅓ p ∙ ⅔ p
   = 1/9 p²   ... (2)

Substitusi persamaan (1) ke persamaan (2) diperoleh:

L = 1/9 ∙ 2x
   = 2x/9

Jadi, luas ∆KMN adalah 2x/9 cm² (B).

Soal No. 49 tentang Fungsi

Jika f(x) = x² − 1 dan g(x) = (x − 2)/(x + 1) maka daerah asal fungsi f ∙ g adalah ….A.   {x│−∞ < x < ∞}
B.   {x│x ≠ −1}
C.   {x│x ≠ 2}
D.   {x│x < −1}
E.   {x│x ≥ 2}

Pembahasan

Daerah asal atau domain suatu fungsi adalah nilai-nilai x yang memenuhi fungsi tersebut.

Mari kita tentukan dulu fungsi yang dimaksud!

Biarkan saja seperti itu, tidak perlu dioperasikan lebih lanjut. Kita hanya mencari tahu, fungsi tersebut memenuhi syarat atau belum.

Karena fungsi f ∙ g berbentuk pecahan maka fungsi tersebut akan memenuhi bila penyebutnya tidak sama dengan nol.

x + 1 ≠ 0
      x ≠ −1

Jadi, daerah asal fungsi f ∙ g adalah {x│x ≠ −1} (B).

Soal No. 50 tentang Statistika

Diketahui median dan rata-rata berat badan 5 balita adalah sama. Setelah ditambahkan satu data berat badan balita, rata-rata meningkat 1 kg, sedangkan mediannya tetap. Jika 6 data berat badan tersebut diurutkan dari yang paling ringan ke yang paling berat maka selisih berat badan antara balita terakhir yang ditambahkan dan balita di urutan ke-4 adalah … kg.A.   4
B.   9/2
C.   5
D.   6
E.   13/2

Pembahasan

Misalkan berat badan 5 bali tersebut adalah:

a, b, c, d, e

Median (nilai tengah) kelima berat badan balita tersebut adalah:

M_d = c

Diketahui median dan rata-rata berat badan 5 balita adalah sama.

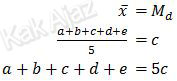
Setelah ditambahkan satu data, misal f, rata-rata meningkat 1 kg.

Tampak bahwa nilai f jauh di atas nilai rata-rata. Jika diurutkan maka f berada di sebelah kanan.

a, b, c, d, e, f

Diketahui bahwa median dari yang telah ditambahkan tersebut nilai tetap sehingga:

         M_d = c
½(c + d) = c
      c + d = 2c
            d = c

Dengan demikian, f dan d adalah:

f − d = c + 6 − c
        = 6

Jadi, selisih berat badan balita terakhir dengan balita urutan ke-4 adalah 6 kg (D).

Bagikan Artikel ini