Pembahasan Matematika SMP UN 2017 No. 26 - 30 - Kumpulan RPP K13

Pembahasan soal Matematika SMP Ujian Nasional (UN) tahun 2017 nomor 26 sampai dengan nomor 30 tentang:

teorema Pythagoras,
kekongruenan,
kesebangunan,
penerapan kesebangunan, dan
unsur-unsur bangun ruang.

Soal No. 26 tentang Teorema Pythagoras

Perhatikan gambar berikut!

Segitiga siku-siku dengan sisi tegak a dan c serta sisi miring b, berlaku hukum Pythagoras, soal matematika SMP UN 2017 no. 26

c² = b² − a²
c² = a² − b²
b² = a² + c²
a² = b² + c²

Dari pernyataan di atas, yang benar adalah ….A.   (1) dan (3)
B.   (2) dan (4)
C.   (2) dan (3)
D.   (3) dan (4)

Pembahasan

Teorema Pythagoras menyatakan bahwa pada segitiga siku-siku:

“Kuadrat sisi miring sama dengan jumlah dari kuadrat kedua sisi tegaknya.”

Berdasarkan gambar di atas, teorema Pythagoras tersebut secara matematis dapat dinyatakan:

b² = a² + c² [pernyataan 3 benar]
a² = b² − c² [pernyataan 4 salah]
c² = b² − a² [pernyataan 1 benar, 2 salah]

Jadi, pernyataan yang benar adalah 1 dan 3 (A).

Soal No. 27 tentang Kekongruenan

Diketahui segitiga KLM dan segitiga PQR kongruen. Besar ∠KLM = 74°, ∠KML = 46°, ∠PQR = 60°, dan ∠PRQ = 46°. Pasangan sisi yang sama panjang pada kedua segitiga itu adalah ….A.   KM = PR
B.   LM = QR
C.   KL = PQ
D.   KM = PQ

Pembahasan

Gambar kedua segitiga tersebut adalah:

Segitiga KLM kongruen dengan segitiga PQR

Berdasarkan gambar kedua segitiga di atas, sisi-sisi yang sama panjang adalah:

KL = PQ [opsi C benar]
LM = PR [opsi B salah]
KM = QR [opsi A dan D salah]

Jadi, pasangan sisi yang sama panjang pada kedua segitiga itu adalah KL = PQ (C).

Soal No. 28 tentang Kesebangunan

Perhatikan gambar berikut!

Trapesium PTUV sebangun dengan trapesium PQRS, soal matematika SMP UN 2017 no. 28, kesebangunan

Trapesium PTUV sebangun dengan trapesium PQRS. Luas daerah trapesium PQRS adalah ….A.   117 cm²
B.   210 cm²
C.   234 cm²
D.   468 cm²

Pembahasan

Pada kedua trapesium di atas, sisi yang bersesuaian adalah:

PS ≅ PV
PQ ≅ PT
SR ≅ VU
QR ≅ TU

Sehingga diperoleh perbandingan:

Perbandingan sisi-sisi trapesium PQRS dan PTUV, kesebangunan

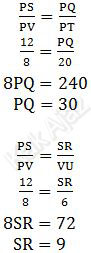
Dengan demikian, ukuran sisi-sisi trapesium PQRS adalah:

Luas trapesium PQRS adalah:

Jadi, luas daerah trapesium PQRS adalah 234 cm² (C).

Soal No. 29 tentang Penerapan Kesebangunan

Perhatikan gambar berikut!

Ukuran foto sebangun dengan bingkai karton, penerapan kesebangunan, soal matematika SMP UN 2017 no. 29

Sebuah foto ditempel pada selembar karton seperti tampak pada gambar. Di sebelah kanan dan kiri foto masih terdapat sisa karton selebar 4 cm. Jika foto dan karton sebangun, luas karton yang tidak tertutup foto adalah ….A.   464 cm²
B.   524 cm²
C.   600 cm²
D.   768 cm²

Pembahasan

Perhatikan gambar di bawah ini!

Berdasarkan gambar di atas diperoleh perbandingan:

Perbandingan ukuran foto dan bingkai karton, rumus kesebangunan

Luas karton yang tidak tertutup foto adalah luas karton dikurangi luas foto.

L' = L_katon − L_foto
    = 60×40 − 48×32
    = 2400 − 1536
    = 864

Jadi, luas karton yang tidak tertutup foto adalah 864 cm² (-).

Soal No. 30 tentang Unsur-unsur Bangun Ruang

Perhatikan gambar bangun kubus berikut!

Bidang diagonal ABGH pada kubus ABCD.EFGH, unsur bangun ruang, soal matematika SMP UN 2017 no. 30

Bidang yang tegak lurus dengan bidang ABGH adalah ….A.   ACGE
B.   BDHF
C.   ADGF
D.   CDEF

Pembahasan

Perhatikan gambar di bawah ini!

Berdasarkan gambar di atas, bidang diagonal ABGH tegak lurus dengan bidang diagonal CDEF.
Jadi, bidang yang tegak lurus dengan bidang ABGH adalah CDEF (D).