Pembahasan Matematika IPA UN: Turunan Fungsi

Pembahasan soal-soal Ujian Nasional SMA-IPA bidang studi Matematika dengan materi pembahasan Turunan Fungsi yang meliputi turunan fungsi aljabar dan trigonometri.

Soal Turunan Fungsi UN 2008

Diketahui

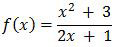
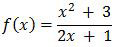
Jika f'(x) menyatakan turunan pertama f(x) maka f(0) + 2f'(0) = ….

A.   –10
B.   –9
C.   –7
D.   –5
E.   –3

Pembahasan

Kita tentukan dulu nilai dari f(0).

Fungsi f(x) berbentuk u/v. Turunan dalam bentuk tersebut dirumuskan:

Misal:

u = x² + 3   →   u' = 2x
v = 2x + 1   →   v' = 2

Sehingga,

Dengan demikian,

f(0) + 2f' (0) = 3 + 2∙(−6)
                   = 3 − 12
                   = −9

Jadi, nilai dari f(0) + 2f' (0) adalah −9 (B).

Terima kasih buat Hendri Kus.

Soal Turunan Fungsi UN 2016

Turunan pertama dari y = sin²⁡(5x − π) adalah ….

A.   y' = −10 sin⁡ (5x − π)
B.   y' = −5 sin⁡ (10x − 2π)
C.   y' = −5 sin (5x − π)
D.   y' = 5 sin⁡ (10x − 2π)
E.   y' = 10 sin⁡ (10x − 2π)

Pembahasan

Fungsi y = sin²⁡(5x − π) terdiri dari 3 fungsi, yaitu fungsi 5x − π, fungsi sinus, dan fungsi sinus kuadrat. Mari kita misalkan terlebih dahulu.

u = 5x − π    → du/dx = 5

v = sin ⁡(5x − π)
v = sin⁡ u      → dv/du = cos ⁡u

y = sin²⁡ (5x − π)
y = v²          → dy/dv = 2v

Dengan demikian,

Nah, sampai di sini kita gunakan rumus:

sin ⁡2α = 2 sin ⁡α cos ⁡α

Dengan demikian, hasil turunan di atas menjadi:

y' = 2 sin ⁡(5x − π)  cos ⁡(5x − π) ∙ 5
    = 2 sin ⁡2(5x − π) ∙ 5
    = 10 5 sin ⁡(10x − 2π)

Jadi, turunan pertama fungsi y adalah opsi (E D).

Soal Turunan Fungsi UN 2006

Turunan pertama dari f(x) = sin⁴⁡ (3x² − 2) adalah f'(x) = ….A.   2 sin²⁡ (3x² − 2) sin⁡ (6x² − 4)
B.   12x sin²⁡ (3x² − 2) sin⁡ (6x² − 4)
C.   12x sin²⁡ (3x² − 2) cos⁡ (6x² − 4)
D.   24x sin³⁡ (3x² − 2) cos² ⁡(3x² − 2)
E.   24x sin³⁡ (3x² − 2) cos (3x² − 2)

Pembahasan

Kita misalkan seperti pada pembahasan soal sebelumnya.

u = 3x² − 2  → du/dx = 6x

v = sin⁡ (3x² − 2)
v = sin⁡ u      → dv/du = cos ⁡u

y = sin⁴⁡ (3x² − 2)
y = v⁴          → dy/dv = 4v³

Dengan demikian,

y' = dy/dx
   = dy/dv ∙ dv/du ∙ du/dx
   = 4v³ ∙ cos ⁡u ∙ 6x
   = 4 sin³⁡ (3x² − 2) ∙ cos (3x² − 2) ∙ 6x
   = 24x sin³⁡ (3x² − 2) ∙ cos (3x² − 2) → (E)

Sampai di sini jawaban sudah ketemu, yaitu opsi E. Tetapi bila diteruskan, jawabannya juga tersedia. Mari kita gunakan rumus sudut ganda.

sin ⁡2α = 2 sin ⁡α cos ⁡α

Untuk memanfaatkan rumus di atas, yang perlu diubah adalah:

• 24x = 12x ∙ 2
• sin³⁡ (3x² − 2) = sin²⁡ (3x² − 2) sin (3x² − 2)

Sehingga turunan fungsi y di atas menjadi:

f'(x) = 12x . 2 sin²⁡ (3x² − 2) sin (3x² − 2) ∙ cos (3x² − 2)
       = 12x sin²⁡ (3x² − 2) 2 sin (3x² − 2) ∙ cos (3x² − 2)
       = 12x sin²⁡ (3x² − 2) sin 2(3x² − 2)
       = 12x sin²⁡ (3x² − 2) sin (6x² − 4)  → (B)

Jadi, turunan pertama dari fungsi f(x) tersebut adalah opsi (B/E).

Soal Turunan Fungsi UN 2007

Turunan pertama dari

adalah f'(x) = ….A.   2/3 cos^−1/3 ⁡3x
B.   2  cos^−1/3 ⁡3x
C.   2/3  cos^−1/3 ⁡3x sin⁡ 3x
D.   -2 cot ⁡3x ∙ ∛(sin² 3x)
E.   2 cot⁡ 3x ∙ ∛(sin² 3x)

Pembahasan

Kita sederhanakan dulu fungsi f(x).

f(x) = ∛(sin² 3x)
      = sin^2/3 3x

Ternyata fungsi f(x) tersebut terdiri dari 3 fungsi, yaitu fungsi 3x, fungsi sinus, dan fungsi sinus pangkat 2/3. Mari kita misalkan ketiga fungsi di atas.

u = 3x       → du/dx = 3

v = sin⁡ 3x
v = sin⁡ u    → dv/du = cos ⁡u

y = sin^2/3 3x
y = v^2/3      → dy/dv = 2/3 v^−1/3

Dengan demikian,

f'(x) = dy/dx
       = dy/dv ∙ dv/du ∙ du/dx
       = 2/3 v^−1/3 ∙ cos ⁡u ∙ 3
       = 2/3 sin^−1/3⁡ 3x ∙ cos 3x ∙ 3
       = 2 sin^−1/3⁡ 3x ∙ cos 3x

Selesai. Tapi tidak ada opsi jawaban yang sesuai. Opsi A, B, dan C sudah pasti salah. Sedangkan opsi D dan E mengandung fungsi cotangent.

Sekarang kita upayakan agar menjadi fungsi cotangent. Kita kalikan dengan sin⁡3x/sin⁡3x .

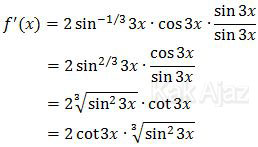
Jadi, turunan pertama dari fungsi f adalah opsi (E).

Soal Turunan Fungsi UN 2007

Jika f(x) = sin²⁡(2x + 1/6 π) maka nilai dari f'(0) = ….A.   2√3
B.   2
C.   √3
D.   1/2 √3
E.   1/2 √2

Pembahasan

Agar soalnya terkesan lebih ramah, kita ganti saja 1/6 π dengan 30° sehingga menjadi:

f(x) = sin²⁡(2x + 30°)

Sekarang kita misalkan seperti pembahasan soal sebelumnya.

u = 2x + 30°  → du/dx = 2

v = sin⁡ (2x + 30°)
v = sin⁡ u        → dv/du = cos ⁡u

y = sin²⁡(2x + 30°)
y = v²            → dy/dv = 2v

Dengan demikian,

f'(x) = dy/dx
       = dy/dv ∙ dv/du ∙ du/dx
       = 2v ∙ cos ⁡u ∙ 2
       = 2 sin⁡ (2x + 30°) ∙ cos (2x + 30°) ∙ 2

Karena yang ditanyakan adalah nilai dari f'(0) maka kita tidak perlu menyederhanakan lagi, cukup dimasukkan x = 0.

f'(0) = 2 sin⁡ (2∙0 + 30°) ∙ cos⁡ (2∙0 + 30°) ∙ 2
       = 4 sin⁡ 30° cos 30°
       = 4 ∙ 1/2 ∙ 1/2 √3
       = √3
Jadi, nilai dari f'(0) fungsi tersebut adalah √3 (C).

Bagikan Artikel ini