Pembahasan Matematika IPA UN 2017 No. 26 - 30 - Kumpulan RPP K13

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPA nomor 26 sampai dengan nomor 30 tentang:

persamaan trigonometri,
perbandingan trigonometri (jumlah dan selisih dua sudut),
perbandingan trigonometri (jumlah dan selisih sinus dan kosinus,
sudut antara garis dan bidang dalam dimensi tiga, serta
jarak antara titik, garis, dan bidang dalam dimensi tiga.

Soal No. 26 tentang Persamaan Trigonometri

Himpunan penyelesaian persamaan cos⁡ 2x − sin ⁡x = 0, untuk 0 ≤ x ≤ 2π adalah ….

A.   {π/6, 5π/6, π}
B.   {π/6, 5π/6, 3π/2}
C.   {π/3, 2π/3, 3π/2}
D.   {π/3, 4π/3, 3π/2}
E.   {7π/6, 3π/2, 11π/6}

Pembahasan

Untuk menyelesaikan soal d atas, trigonometrinya harus dijadikan sejenis. Dalam hal ini, cos⁡ 2x harus diubah menjadi bentuk sinus.

cos⁡ 2x = 1 − 2 sin² ⁡x

Sehingga soal di atas menjadi:

             cos⁡ 2x − sin ⁡x = 0
     1 − 2 sin² ⁡x − sin⁡ x = 0
     2 sin² ⁡x + sin⁡ x − 1 = 0
(2 sin ⁡x − 1)(sin⁡ x + 1) = 0
sin⁡ x = 1/2 atau sin⁡ x = −1

Untuk sin⁡ x = 1/2 (positif), nilai x berada pada kuadran I dan II.

sin⁡ x = 1/2
sin⁡ x = sin⁡ 30°

Kuadran I x = 30°
= π/6

Kuadran II x = 180° − 30°
= 150°
= 5π/6

Sedangkan untuk sin⁡ x = −1 hanya mempunyai satu nilai pada interval 0 ≤ x ≤ 2π.

sin ⁡x = −1
x = 270°
= 3π/2

Dengan demikian, penyelesaiannya adalah:

π/6, 5π/6, 3π/2

Jadi, himpunan penyelesaian dari persamaan trigonometri tersebut adalah opsi (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan Trigonometri.

Soal No. 27 tentang Perbandingan Trigonometri (jumlah dan selisih dua sudut)

Diketahui sin⁡ α cos ⁡β = 2/5 dan (α + β) = 5π/6. Nilai sin⁡(α − β) = ….A.   −1/2
B.   −3/10
C.   −1/10
D.   3/10
E.   1/2

Pembahasan

Langkah pertama, kita ubah sudut radian ke dalam derajat, supaya lebih familiar di otak kita.

(α + β) = 5π/6
= 150°

Selanjutnya kita gunakan rumus jumlah dua sudut.

sin⁡(α + β) = sin⁡ α cos ⁡β + cos⁡ α sin ⁡β
    sin⁡ 150° = 2/5 + cos⁡ α sin⁡ β
            1/2 = 2/5 + cos⁡ α sin⁡ β
cos⁡ α sin⁡ β = 1/2 − 2/5
                  = 1/10

Sekarang kita masuk ke pertanyaan.

sin⁡(α − β) = sin⁡ α cos⁡ β − cos ⁡β sin⁡ α
                 = 2/5 − 1/10
                 = 4/10 − 1/10
                 = 3/10

Jadi, nilai sin⁡(α − β) adalah 3/10 (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Perbandingan Trigonometri.

Soal No. 28 tentang Perbandingan Trigonometri (jumlah dan selisih sinus dan kosinus)

Nilai dari

(sin⁡ 280° - sin⁡ 140°)/(cos⁡ 280° - cos⁡ 140° ) = ⋯.Selisih sinus dan kosinus, soal UN 2017

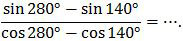
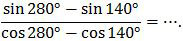
A.   −√3
B.   −√2
C.   −1/2 √3
D.   √2
E.   √3

Pembahasan

Untuk menyelesaikan soal di atas, sebaiknya dihafal rumus selisih sinus dan kosinus berikut ini.

sin⁡ A − sin ⁡B = 2 cos⁡ ½ (A + B) sin⁡ ½ (A − B)
cos ⁡A − cos⁡ B = −2 sin ½ (A + B) sin⁡ ½ (A − B)

Dengan demikian penyelesaian soal di atas adalah:

Tahap penyelesaian soal selisih sinus dan kosinus UN 2017

Sudut 210° masuk dalam kuadran III sehingga bisa diganti 180° + 30°. Rumus sinus dan kosinus dalam kuadran III adalah:

sin⁡(180° + α) = −sin ⁡α
cos⁡(180° + α) = −cos ⁡α

Sehingga penyelesaian di atas dapat dilanjutkan menjadi:

Penyelesaian akhir soal selisih sinus dan kosinus UN 2017

Jadi, nilai dari perbandingan trigonometri tersebut adalah −√3 (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Perbandingan Trigonometri.

Soal No. 29 tentang Sudut antara Garis dan Bidang dalam Dimensi Tiga

Diketahui kubus ABCD.EFGH dengan panjang rusuknya 6 cm. Jika α adalah sudut antara bidang AFH dan bidang BDHF, nilai sin ⁡α = ….A.   1/2
B.   1/3 √3
C.   1/2 √2
D.   1/2 √3
E.   2/3 √2

Pembahasan

Perhatikan ilustrasi gambar untuk soal di atas!

Sudut antara bidang AFH dan bidang BDHF dalam kubus ABCD.EFGH

Misalkan panjang sisi kubus tersebut adalah a. Panjang PQ sama dengan panjang sisi kubus sedangkan panjang AQ sama dengan setengah diagonal bidang. Sehingga: