Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2016 Kode Naskah 321
Jumat, 25 Mei 2018
Tambah Komentar
Pembahasan soal Matematika Dasar Tes Kemampuan Potensi Akademik (TKPA)
Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2016 kode
naskah 321 nomor 46 sampai dengan nomor 50 tentang:
- persamaan kuadrat,
- eksponen,
- persamaan garis lurus,
- pertidaksamaan, dan
- transformasi geometri.
Soal No. 46 tentang Persamaan Kuadrat
Misalkan m dan n adalah bilangan bulat dan merupakan akar-akar persamaan x2 + ax − 30 = 0 maka nilai a agar m + n maksimum adalah ….
A. 30
B. 29
C. 13
D. −29
E. −31
B. 29
C. 13
D. −29
E. −31
Pembahasan
Persamaan kuadrat x2 + ax − 30 = 0 mempunyai akar m dan n. Perkalian kedua akarnya adalah:
mn = c/a
mn = −30 … (1)
mn = −30 … (1)
Sedangkan penjumlahan kedua akarnya adalah:
m + n = −b/a
m + n = −a … (2)
m + n = −a … (2)
Sekarang perhatikan persamaan (1). Perkalian m dan n yang menghasilkan −30 adalah:
| −30 | m + n | |
| m | n | |
| −1 | 30 | 29 |
| 1 | −30 | −29 |
| −2 | 15 | 13 |
| ⋮ | ⋮ | ⋮ |
Berdasarkan tabel di atas, tampak bahwa nilai maksimum untuk m + n adalah 29.
Kita gunakan persamaan (2) untuk mendapatkan nilai a.
m + n = −a
29 = −a
a = −29
29 = −a
a = −29
Jadi, nilai a agar m + n maksimum adalah −29 (D).
Soal No. 47 tentang Eksponen
Jika A2x = 2 maka

A. 31/18
B. 31/9
C. 32/18
D. 33/9
E. 33/18

A. 31/18
B. 31/9
C. 32/18
D. 33/9
E. 33/18
Pembahasan
Diketahui.
A2x = 2
Kunci penyelesaian soal di atas adalah menghilangkan pangkat negatif terkecil, yaitu A−5x. Caranya adalah dengan mengalikan A5x.

Selanjutnya, kita substitusikan A2x = 2 pada hasil di atas.

Jadi, nilai dari bentuk pangkat tersebut adalah 31/18 (A).
Soal No. 48 tentang Persamaan Garis Lurus
Suatu garis yang melalui titik (0, 0) membagi persegi panjang dengan
titik-titik sudut (1, 0), (5, 0), (1, 12), dan (5, 12) menjadi dua
bagian yang sama luas. Gradien garis tersebut adalah ….A. 1/2
B. 1
C. 2
D. 12/5
E. 3
B. 1
C. 2
D. 12/5
E. 3
Pembahasan
Perhatikan gambar di bawah ini!

Gradien garis OP adalah:

Sedangkan gradien garis OQ adalah:

Karena OP segaris dengan OQ maka gradien kedua garis tersebut adalah sama.
mP = mQ
m = (12 − m)/5
5m = 12 − m
6m = 12
m = 2
m = (12 − m)/5
5m = 12 − m
6m = 12
m = 2
Jadi, gradien garis yang membagi persegi panjang tersebut adalah 2 (C).
Soal No. 49 tentang Pertidaksamaan
Semua bilangan real x yang memenuhi
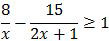
adalah ….A. −2 ≤ x ≤ 2
B. x ≤ −2 atau 0 ≤ x < 1
C. −2 ≤ x < −1/2 atau 0 < x ≤ 2
D. −2 ≤ x < −1/2 atau x ≥ 2
E. x ≤ −2 atau x ≥ 2
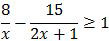
adalah ….A. −2 ≤ x ≤ 2
B. x ≤ −2 atau 0 ≤ x < 1
C. −2 ≤ x < −1/2 atau 0 < x ≤ 2
D. −2 ≤ x < −1/2 atau x ≥ 2
E. x ≤ −2 atau x ≥ 2
Pembahasan
Pertidaksamaan bentuk pecahan yang menggunakan tanda pertidaksamaan ‘≤’
atau ‘≥’ harus memperhatikan syarat pecahan, yaitu penyebut suatu
pecahan tidak boleh sama dengan nol.
I. x ≠ 0
II. 2x + 1 ≠ 0
x ≠ −1/2
x ≠ −1/2
Berdasarkan kedua syarat penyebut di atas, sudah pasti opsi A dan B salah. Hal ini karena x = 0 dan x = −1/2 masuk dalam interval kedua opsi tersebut.
Mari kita kerjakan pertidaksamaan di atas. Langkah pertama adalah
memindahkan semua suku ke ruas kiri sehingga ruas kanan menjadi nol.

Selanjutnya kita samakan semua penyebutnya.

Sekarang tinggal kita faktorkan dengan menggunakan rumus a2 − b2 = (a + b)(a − b).

Pembuat nol pertidaksamaan di atas adalah:
x = −2
x = 2
x = 0
x = −1/2
x = 2
x = 0
x = −1/2
Berdasarkan pembuat nol tersebut dapat dibuat garis bilangan sebagai berikut:

Diperoleh:
−2 ≤ x ≤ −1/2 atau 0 ≤ x ≤ 2
Karena pertidaksamaan tersebut mempunyai syarat x ≠ 0 dan x ≠ −1/2 maka tanda pertidaksamaan ‘≤’ yang berhubungan dengan 0 dan 1/2 harus diubah menjadi ‘<’.
Sehingga hasil akhirnya adalah:
−2 ≤ x < −1/2 atau 0 < x ≤ 2
Jadi, semua bilangan real x yang memenuhi pertidaksamaan tersebut adalah opsi (C).
Soal No. 50 tentang Transformasi Geometri
Jika grafik fungsi y = x2 − (9 + a)x + 9a diperoleh dari grafik fungsi y = x2 − 2x − 3 melalui pencerminan terhadap garis x = 4 maka a = ….
A. 7
B. 5
C. 3
D. −5
E. −7
B. 5
C. 3
D. −5
E. −7
Pembahasan
Pencerminan terhadap garis x = h dirumuskan:
P(x, y) → P'(2h − x, y)
Sehingga pencerminan terhadap x = 4 adalah:
P(x, y) → P' (8 − x, y)
Berdasarkan pencerminan tersebut diperoleh:
x' = 8 − x atau x = 8 − x' … (1)
y' = y atau y = y' … (2)
y' = y atau y = y' … (2)
Substitusi persamaan (1) dan (2) ke fungsi asal diperoleh:
y = x2 − 2x − 3
y' = (8 − x')2 − 2(8 − x') − 3
= 64 − 16x' + (x')2 − 16 + 2x' − 3
= (x')2 − 14x' + 45
y' = (8 − x')2 − 2(8 − x') − 3
= 64 − 16x' + (x')2 − 16 + 2x' − 3
= (x')2 − 14x' + 45
Dengan demikian, bayangan dari fungsi tersebut adalah:
y = x2 − 14x + 45
Nah, sekarang bandingkan bayangan fungsi tersebut dengan fungsi yang disajikan pada soal.
y = x2 − 14x + 45
y = x2 − (9 + a)x + 9a
y = x2 − (9 + a)x + 9a
Diperoleh:
9 + a = 14
a = 5
a = 5
atau
9a = 45
a = 5
a = 5
Jadi, nilai a pada grafik fungsi hasil pencerminan tersebut adalah 5 (B).


Belum ada Komentar untuk "Pembahasan Matematika Dasar No. 46 - 50 TKPA SBMPTN 2016 Kode Naskah 321"
Posting Komentar